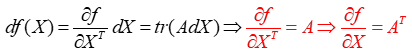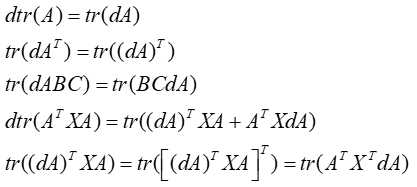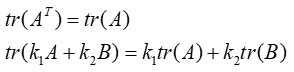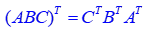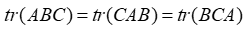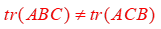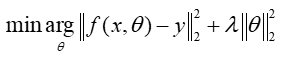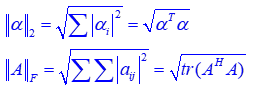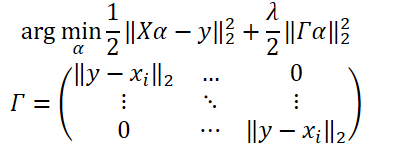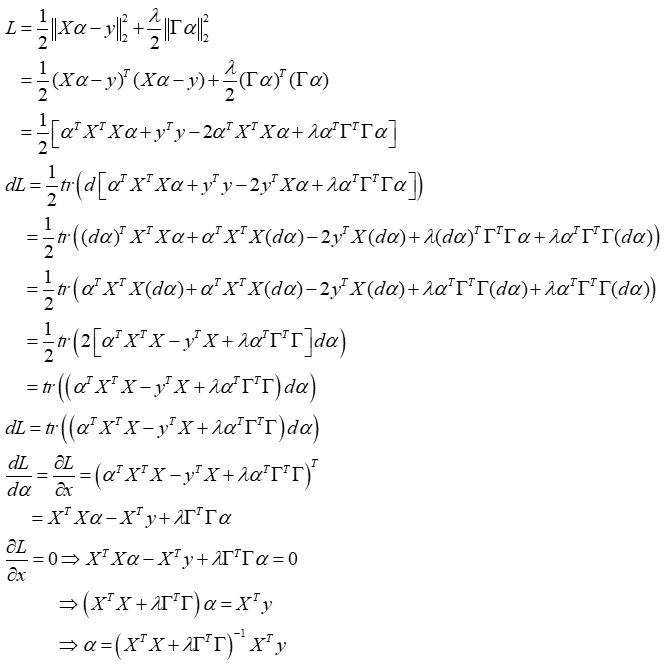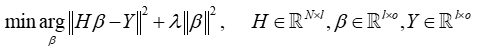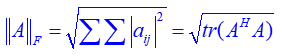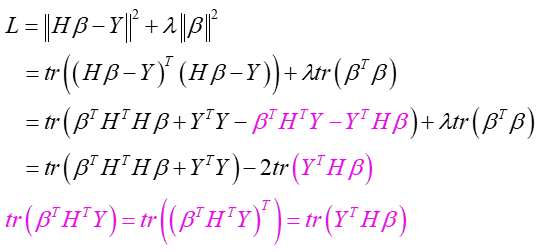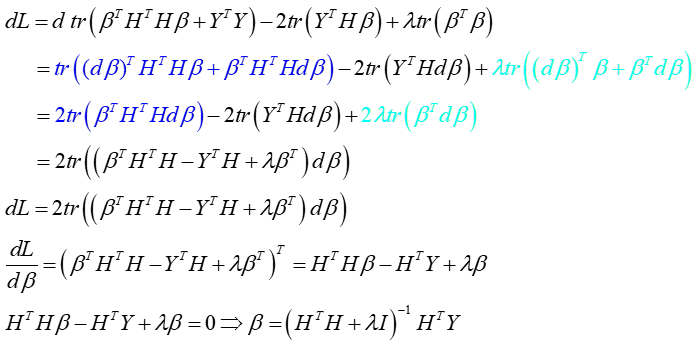基础知识（标量函数对矩阵变量/向量求导）

• 核心：使用矩阵微分与trace的关系

函数f微分=Jacobian矩阵*X的微分

注意：最后求得导数需要去掉trace，因为是标量所以可以直接去掉，但结果需要装置

• 常用基础公式

trace的循环不变性，A，B，C为方阵，但更一般的如果ABC不是方阵但其循环后矩阵乘法存在，则下列公式依旧成立

但是一般以下是不成立的

• 机器学习常用损失函数形式

也就是说损失函数一般写为矩阵/向量变量的标量函数，通过矩阵/向量范数即可去掉范数求解中的绝对值，一般考虑向量L2范数和矩阵F范数

Example 1：L2范数约束下带Tikhonov regularization的稀疏表示

​​​​​​​

Example 2： ELM 约束求解（ridge regression岭回归）

注：上式参数均为矩阵，与稀疏表示区别，所以这里的范数通常为矩阵的F范数，如下

将上式写为损失函数的形式并展开（这样做是为了使函数可导，与稀疏类似）

矩阵范数的展开与向量稍有不同，这里借助F范数的trace表达去掉绝对值

对L求导：